La versión moderna de la teoría de cuerdas (ST), también llamada teoría M (MT), es un marco teórico que apunta a la existencia de una teoría cuántica no perturbativa ST/MT de la que sólo conocemos algunas descripciones clásicas perturbativas, que sabemos cuantizar y que están conectadas entre sí por dualidades. Por ello, el concepto de dualidad permea todo el marco teórico ST/MT, desde los fundamentos hasta las aplicaciones.
Por ahora todas las dualidades son conjeturas matemáticas. Por ello muchos físicos consideran la teoría ST/MT como, simplemente, matemáticas. Pero no debemos olvidar que gran parte de la intuición física en la teoría ST/MT se obtiene gracias a las dualidades. Quizás por ello desde hace unos años (tras la segunda revolución de la teoría de cuerdas en 1994 que llevó al nacimiento de la teoría M) se pensaba que eran la guía hacia la formulación cuántica no perturbativa de la teoría ST/MT.
Nos revisa de forma exquisita la situación actual de las dualidades en teoría ST/MT el genial Joseph Polchinski, “Dualities,” arXiv:1412.5704 [hep-th]. Te recomiendo aprovechar estas fechas navideñas para disfrutar, con turrón o con mantecados, de dicho artículo.
Como es de esperar, el artículo ha generado un intenso debate en el blog de Peter Woit, “Dualities,” Not Even Wrong, 19 Dec 2014. Te recomiendo ojearlo si te interesan este tipo de debates en pro y en contra de un concepto que podría ser fundamental, o quizás sólo una cortina de humo que desvía nuestra atención hacia el espacio, alejándola del tiempo. Me refiero a que algunas dualidades, como la dualidad S, apuntan a que el espacio es un concepto clásico emergente en teoría ST/MT, pero ninguna dualidad, por ahora, apunta a cómo emerge el tiempo (que en física cuántica tiene un status especial).
La idea de dualidad es muy antigua, se remonta a finales del siglo XIX. La solución de una ecuación diferencial con un parámetro ε~O(1) se construye mediante el acoplo (matching, no confundir con el concepto que se usa en teoría cuántica de campos) de dos aproximaciones asintóticas complementarias (duales) para ε→0, y para 1/ε→0 (es decir, ε→∞). Ambas describen la misma física (lo más correcto sería decir que el mismo problema matemático), pero desde un punto de vista diferente. En muchas ramas de la física clásica se usa esta técnica matemática, pero donde más brilla, por ser casi imprescindible, es en física de fluidos (y sus derivados, física de plasmas, magnetohidrodinámica estelar, etc.).
En teoría cuántica de campos (QFT), teoría de cuerdas y teoría M el problema es que desconocemos la teoría clásica (no perturbativa) que describe la física cuántica para g~O(1), donde g es el parámetro de acoplo asociado a los estados de la teoría que no corresponden al estado de vacío. Se conjetura que dicha teoría existe porque somos capaces de construir las versiones cuánticas de dos teorías clásicas (perturbativas) que parecen describir la misma física para g→0, y para 1/g→0. Puede que no exista la teoría clásica no perturbativa que buscamos, pero en la actualidad no sabemos hacer física cuántica sin una teoría clásica subyacente que la soporte (salvo en ciertas excepciones de juguete que confirman la regla). Y por supuesto puede que dicha teoría, si existe, no sea única.
La teoría clásica sobre la que se construye una QFT se describe mediante un lagrangiano (o una acción, su integral en el tiempo). Sabemos cuantizar dicha teoría usando integrales de camino, cuantización canónica u otras técnicas más exóticas. Sin embargo, muchas teorías clásicas no tienen formulación lagrangiana y por ello no sabemos cuantizarlas. Aún así la esperanza es obtener un lagrangiano que describa la teoría ST/MT. Quizás no exista. O quizás las dualidades no aportan información relevante a la hora de construir dicho lagrangiano. A día de hoy no lo sabemos, pero por desgracia no conocemos otro camino para seguir avanzando.
Considera esta figura tridimensional imposible. Una dualidad entre el extremo izquierdo y el extremo derecho de la figura podría ser una transformación topológica que deforme las tres secciones circulares en tres secciones cuadradas y que pegue las tres en una viga rectangular como la del extremo derecho (relee esta frase hasta entender lo que quiero decir). Dicha dualidad entre la parte izquierda y la parte derecha podría sugerir que existe un objeto “real” entre ambos extremos. Sin embargo, vemos en esta figura que dicho objeto es imposible de construir. No existe. Algo parecido podría ocurrir en la teoría ST/MT con las dualidades que se han conjeturado.
Una teoría clásica perturbativa para un campo φ se describe por un lagrangiano L(φ) = L0(φ) + g L1(φ) + O(g²), donde g es la constante de acoplo. El estado de vacío del campo es descrito por L0(φ), el estado con partículas en interacción a nivel de árbol (tree level) por L1(φ), siendo los estados con interacción a nivel de lazos (loops) descritos por términos de mayor orden, sean O(g²). Otra teoría clásica perturbativa estará descrita por otro lagrangiano L’(φ’) = L0‘(φ’) + g’ L1‘(φ’) + O(g’²). Ambas teorías son duales (se suele hablar de dualidad S) cuando para g = 1/g’ hay un diccionario que asocia todos los estados cuánticos del campo φ con estados del campo φ’ (en la mayoría de los casos de interés quedan estados sin asociar que se conjetura que corresponden a estados de la otra teoría que aún son desconocidos, pero cuya existencia queda garantizada por la propia dualidad).
La dualidad es útil porque el límite de acoplo fuerte para la teoría L, dado por g→∞, se puede describir por el límite de acoplo débil para la teoría L’, dado por g’→0, y viceversa. Una teoría perturbativa nos permite calcular la física para acoplo débil, pero no aporta información para acoplo fuerte. Por ello, la conjetura de la dualidad entre ambas teorías tiene una gran utilidad práctica (permite calcular la física para acoplo fuerte de una teoría usando la física para acoplo débil de la teoría dual). Por supuesto, el régimen g=O(1), o g’=O(1), queda fuera de lo que suele abarcar la dualidad.
En el contexto de la teoría ST/MT el interés de la dualidad va más allá de una simple herramienta de cálculo. La conjetura fundamental es que existe una teoría M(Ψ) no perturbativa caracterizada por un parámetro α tal que en cierto límite conduce a α→g y M(Ψ)→L(φ), y en otro límite α→g’ y M(Ψ)→L’(φ’). Notarás que uso la letra M en lugar de la letra L para dicha teoría; la razón es que no quiero sugerir que se puede asociar un lagrangiano a la teoría M(Ψ), porque podría no existir. También he cambiado la constante de acoplo g por una constante de acoplo α porque su relación puede ser altamente no trivial (incluso inexistente, salvo en los límites indicados). Por supuesto, mientras no se describa de forma explícita la teoría M, a día de hoy, todas estas dualidades son conjeturas razonables guiadas por la intuición física y el formalismo matemático.
Lo maravilloso de las dualidades son los milagros. Parece milagroso que ciertos cálculos realizados con pies en el fango, pero guiados por una dualidad, ofrezcan la respuesta correcta (a veces ha costado muchos años demostrar que la respuesta ST/MT a un problema concreto era correcta y en muchos casos aún no se ha logrado). El mayor milagro es que, los cuerdistas tienen una suerte milagrosa, hasta ahora la teoría ST/MT no ha fallado nunca. Nadie sabe el porqué, pero la esperanza (casi navideña) es que la razón sea que la teoría ST/MT es la teoría final de todo. Por supuesto, esta utopía tiene muchos detractores.
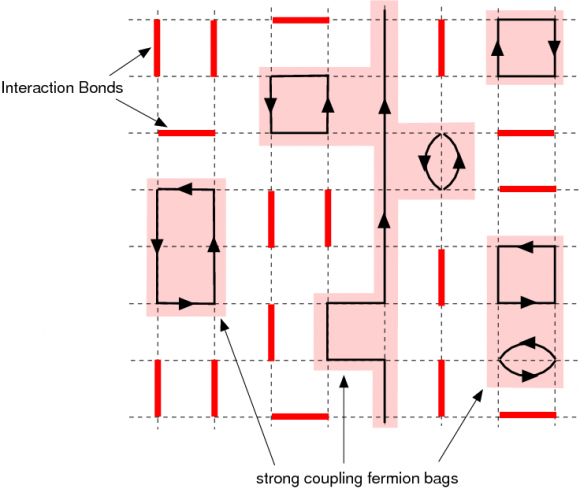
Hay problemas muy sencillos (toy models) en los que la dualidad funciona a la perfección (es decir, hay un teorema de dualidad en lugar de una conjetura de dualidad). Los ejemplos más conocidos son problemas integrables en los que la teoría M(Ψ) es resoluble para todo α, como el modelo de Ising bidimensional (una red cuadrada discreta de espines acoplados a pares). Otro ejemplo muy bonito es la equivalencia demostrada por Sidney Coleman entre el modelo masivo de Thirring (que describe partículas de tipo fermión) y la ecuación escalar de sine-Gordon (que describe partículas de tipo bosón); que las parejas de fermiones se comporten como bosones parece obvio, pero que ciertas soluciones bosónicas se comporten como fermiones es realmente inesperado y sugerente, si no conoces los detalles matemáticos parece milagoroso.
Una dualidad más interesante es la que existe entre campos eléctricos y campos magnéticos en la teoría de Maxwell para el electromagnetismo. Para campos libres (en el vacío sin partículas) esta dualidad es exacta, pero si hay partículas con carga eléctrica la teoría dual debe contener monopolos magnéticos; esta dualidad tiene como valor añadido que predice que la carga eléctrica (y la carga magnética) está cuantizada. Una dualidad similar existe en la cromodinámica cuántica (QCD) que describe la interacción entre quarks y gluones. La dualidad entre campos cromoeléctrico y cromomagnético se pensó, hace décadas, que permitiría entender el confinamiento (un fenómeno asociada a acople fuerte); por desgracia, no se ha podido avanzar mucho en este camino y el confinamiento sigue siendo una conjetura (desde el punto de vista matemático, ya que desde el punto de vista físico está más que demostrado en los experimentos realizados en los últimos 40 años).
La adición de la supersimetría a una teoría de Yang-Mills (como QCD) abre todo un mundo de posibles dualidades, sobre todo cuando el número de dimensiones del espaciotiempo es mayor de cuatro. Diferentes manera de compactificar las dimensiones extra dan lugar a diferentes dualidades gracias a la supersimetría. Esta rica y extensa red de dualidades no ha pasado del estado de conjetura, pero muchos creen que esconde algo muy relevante. De hecho, hace 20 años se pensaba que sería el germen de una teoría unificada de todo, quizás la teoría definitiva. Hoy en día nos limitamos a disfrutar de su belleza matemática. Las historias de milagros tienen mucho atractivo, yo diría que los milagros son bellos en esencia.
En teoría de cuerdas la gravedad está asociada a las cuerdas cerradas y el resto de las interacciones fundamentales a las cuerdas abiertas. Consideremos una teoría cuántica de campos en un espaciotiempo de
dimensiones, con 
dimensiones compactas (de radio finito) y 
dimensiones no compactas (de radio infinito). Una partícula encerrada en una caja periódica con periodo 
presenta estados de la forma 
para 
entero, que tienen momento 
y energía 
donde
es el momento en las dimensiones no compactas y 
es la masa en reposo. Esta energía diverge para 
, salvo para el vacío 
. De hecho, para energías por debajo de 
el campo se propaga en las dimensiones no compactas, como si las dimensiones compactas no existieran. Para una cuerda cerrada encerrada en la misma caja se tiene que la energía
cuyos dos primeros términos coinciden con la fórmula de arriba, el último es un término de masa y la única novedad es el tercer término cuyo origen es específico de una teoría de cuerdas (cerradas). En concreto
es el número de giros del campo en las dimensiones compactas (winding number). Para , los estados con 
corresponden al límite de muy alta energía, pero están acompañados de estados con 
de muy baja energía. Todo lo contrario ocurre en el límite opuesto 
, los estados son de muy baja energía y los estados de muy alta energía. Esta dualidad entre valores grandes de 
y valores pequeños , bajo el intercambio 
, junto a 
, se denomina dualidad T y se interpreta como que las cuerdas (cerradas) ven el espaciotiempo de forma diferente a las partículas. Hay una longitud mínima dada por el valor autodual, es decir, 
. No existen las longitudes más pequeñas y a esta escala emerge el espaciotiempo a partir de la interacción dinámica entre las cuerdas cerradas. Hay que recordar que para cuerdas abiertas se tiene
expresión que no tiene término en
(no hay winding number). Por supuesto, todas las teoría con cuerdas abiertas presentan cuerdas cerradas (siempre se puede cerrar una abierta). La interpretación de estas fórmulas en un espaciotiempo con dimensiones de las cuales son compactas es que las cuerdas cerradas se mueven en las dimensiones, pero las cuerdas abiertas sólo en las dimensiones. Por tanto, las cuerdas abiertas tienen sus extremos conectados a membranas con 
dimensiones espaciales (que Polchinski bautizó como D-branas (D-branes), donde la D se refiere a que se usan condiciones de contorno de Dirichlet). Las dualidades mostraron que la teoría ST/MT incluye, además de las cuerdas, otros objetos extensos llamados branas. La intuición sobre la teoría ST/MT que nos han ofrecido las dualidades nos ha llevado a soñar con una teoría final, una teoría de todo. Sin embargo, también nos ha hecho caer en una trampa, el problema del landscape. Las dualidades dependen de cómo se compactifiquen las dimensiones extra del espaciotiempo y el número de posibilidades excede el poder de las matemáticas actuales. Nos gustaría que existieran leyes físicas (o resultados matemáticos) que sesgaran el landscape y nos guiaran hacia la respuesta. Pero por ahora su existencia es pura utopía.
No te aburro más. Fin de año es época de buenos propósitos, algunos que rayan la utopía. Ed Witten decía que la teoría de cuerdas era física del siglo XXI caída de forma milagrosa en el siglo XX. Albert Einstein decía que la naturaleza puede ser perversa, pero no maliciosa. El gran problema de la teoría ST/MT es que las matemáticas del siglo XXI son pura utopía a principios de este siglo. Felices fiestas y disfruta del artículo de Polchinski en estas fechas. Recuerda, es más fácil de leer de lo que crees (aunque ciertos pasajes son de alto nivel técnico). Obvia decir que no olvides acompañarlo de cava y turrrón, si te apetece.
La Ciencia de la Mula Francis
No hay comentarios