Hay señales de la existencia de física no descrita por el modelo estándar que son muy obvias (como la energía oscura y la materia oscura) y otras que son muy sutiles, como la anomalía en el momento magnético anómalo del muón (g-2)μ. Las medidas experimentales muestran una desviación a 3,6 σ respecto a la predicción del modelo estándar, aunque el error experimental de 0,5 ppm (partes por millón) es similar al error teórico (que para las correcciones hadrónicas es de 0,45 ppm). Hay varios experimentos que pretenden reducir el error experimental y varios grupos de teóricos que pretenden reducir el error en el cálculo de las contribuciones hadrónicas. Yo destacaría el nuevo experimento E989 en el Fermilab para la medida de g-2 (ya hablé de su posible transporte en helicóptero en 2013, que al final ha sido cancelado), que empezará a tomar datos en 2016 y alcanzará un error de 0,14 ppm (lo que verificará la anomalía entre teoría y experimento con entre 5 y 9 σ, caso de que persista). Nos lo ha contado Mark Lancaster (University College London, On Behalf of E989 Collaboration), “The New Muon g-2 Experiment,” Photon-2013, Paris 20-24 May 2013 [slides].
La figura que abre esta entrada es la nueva medida experimental de (g-2) obtenida por el detector KLOE en el colisionador electrón contra positrón DAFNE, que nos ha contado A. Passeri (on behalf KLOE collaboration), “Measurement of the hadronic cross sections at KLOE with ISR and their impact to the muon anomaly and U-boson search,” Photon-2013, Paris 20-24 May 2013 [slides].
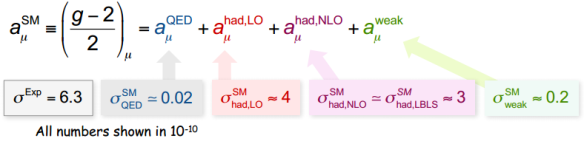
Los cálculos hadrónicos son difíciles, como nos cuentan Zhiqing Zhang (LAL, Orsay), “Review of Recent Leading-Order Hadronic Vacuum Polarization Calculation,” Photon 2013, 22 May [slides]; Vladyslav Pauk, “Gamma-gamma sum rules and their implication on the hadronic LbL contribution to (g-2)μ,” Photon 2013, 22 May [slides]; Arkady Vainshtein, “Hadronic Light-by-Light Scattering in the Muon Anomalous Magnetic Moment,” Photon 2013, 22 May [slides].
¿Podría ocurrir que la anomalía entre el valor experimental y el valor teórico sea debida al cálculo de las contribuciones hadrónicas? Mucha gente así lo cree. De hecho, un nuevo cálculo teórico, aún en curso, apunta a su reducción a sólo 2,4 σ, como nos cuenta H. Spiesberger, “Muon g-2 and QCD Sum Rules,” Photon 2013, 22 May [slides]. Habrá que estar al tanto de estos progresos teóricos. ¿Cuándo seremos capaces de obtener una precisión en QCD a baja energía similar a la que se obtiene en QED? Quizás sea una utopía pensar que algún día podremos calcular el momento magnético anómalo del muón con precisión similar al del electrón (g-2) = 0,002 319 304 361 46 ± 0.000 000 000 000 56, valor obtenido con la QED a quinto orden (NNNNLO) por T. Kinoshita y sus colegas.
Por cierto, quizás te preguntes qué es el momento magnético anómalo del muón. Permíteme una discusión breve. Una carga eléctrica en un campo magnético siente una fuerza que es proporcional a una magnitud llamada momento magnético. Los niveles atómicos de los electrones en un átomo inmerso en un campo magnético se desdoblan por efecto Zeeman. Este desdoblamiento depende del momento magnético del electrón, que tiene dos componentes, una proporcional el momento angular orbital (con constante de proporcionalidad g=1) y otra proporcional al momento de espín (con constante de proporcionalidad g=2). El vacío en electrodinámica cuántica (QED) introduce correcciones radiativas en el momento magnético de espín del electrón, resultando un valor de (g-2) diferente de cero, lo que se denomina momento magnético anómalo (normalmente se calcula el valor de la constante a = (g-2)/2). La constante adimensional (g-2) determina el valor del momento magnético para cualquier leptón (electrón, muón y leptón tau). La predicción teórica en QED es una función de la constante de estructura fina <α y de los cocientes entre las masas de los tres leptones.
Para el electrón la predicción de la QED da un resultado con un error de 0,3 ppb (partes por mil millones) más preciso que el medido en los experimentos (unos 0,7 ppb). Sin embargo, para el muón el cálculo teórico es más complicado porque es necesario incluir en los loops de las correcciones radiativas los efectos electrodébiles (EW) debidos a los bosones W, Z y Higgs, y los efectos hadrónicos (QCD) debidos a los quarks u (arriba), d (abajo) y s (extraño), los que tienen una masa menor que el muón. El error teórico para las correcciones QED es de 0,3 ppb, enorme comparado con el error experimental de unos 0,5 ppm (partes por millón). Para las correcciones EW el error teórico es de 0,01 ppm, también muy inferior al experimental. Pero las correcciones hadrónicas son muy difíciles de calcular (de hecho ni siquiera conocemos el valor exacto de la masa de los quarks) y el error teórico es de 0,42 ppm, un error comparable el del resultado experimental (unos 0,5 ppm).
Francis (th)E mule Science's News














No hay comentarios